지나가던 개발자
[Python] 백준 2747번(피보나치 수) 문제 풀이 본문
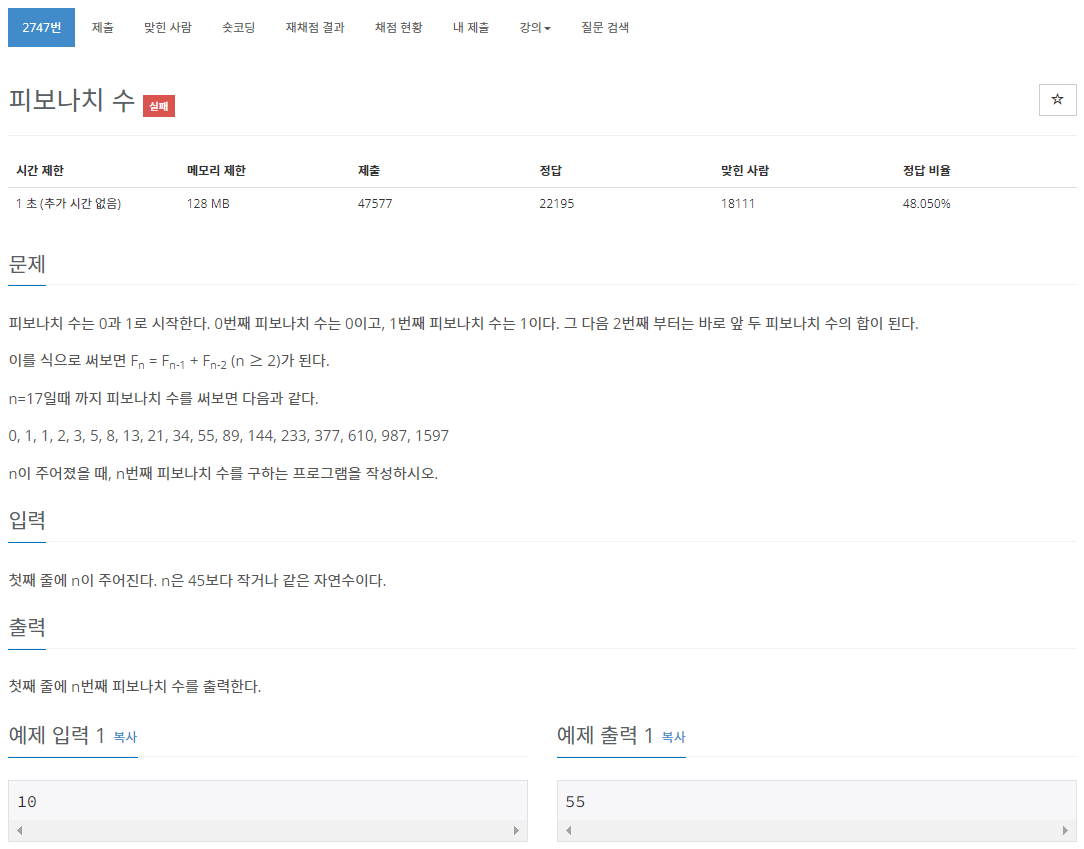
백준의 2747번 문제 풀이이다. 피보나치 수인데, 이런 문제로 굉장히 많이 나와가지고 그냥 한번 풀어 봐야겠다.
피보나치 수는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다. 예를 들어 [1, 1] 다음에는 1+1이니 2가 들어가서 [1, 1, 2], 다음에는 1+2니까 [1, 1, 2, 3, ...] 이런식으로 계속 가는 수열을 말한다.
따라서 이 원리대로 코드를 작성하여 보자.
n = int(input())
fibonacci_numbers = [1, 1]
i = 2
while True:
fibonacci_numbers.append(fibonacci_numbers[i-1] + fibonacci_numbers[i-2])
i += 1
if len(fibonacci_numbers) == n:
break
print(fibonacci_numbers[-1])
이렇게 코드를 작성하였다. 입력받은 수만큼 피보나치 수열 리스트를 만들어 출력하는 프로그램이다. 분명히 출력이 잘 되는 것까지 내 두 눈으로 확인했다. 그런데 백준에 제출하여 보니,

메모리 초과... 코드를 다시 짜야 한다는 뜻이다. 메모리 초과가 안되게.
그래서 다시 짜 보았다.
n = int(input())
fn = 1
fn1 = 1
fibonacci_number = 2
i = 2
while True:
fibonacci_number = fn + fn1
fn = fn1
fn1 = fibonacci_number
i += 1
if i == n:
break
print(fibonacci_number)
이번에는 리스트 대신에 변수들을 사용해서 메모리를 낮췄다 생각했다. 그래서 다시 제출해봤다.

이번에는 뭔 시간 초과가 뜬다. 시간 초과는 또 뭔지 모르겠다.
그 말은 코드를 또 다시 짜야 한다는 뜻이다.
n = int(input())
fibonacci_numbers = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 98, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170]
print(fibonacci_numbers[n-1])
이번에는 조금 원시적인 방법을 써봤다. n은 45보다 작거나 같으니까, 45 길이의 피보나치 수열을 넣은 다음에 그를 출력하는 것이다.

근데 이건 그냥 틀렸다 나온다. 뭐가 문제지.
원시적인 방법은 포기하고 다시 논리적인 사고를 통해 이 오류들을 해결할 방안들을 모색해 봤다.
다음 날, 나는 아주 획기적인 방법을 고안했다. 변수 두 개만 가지고 피보나치 수열을 구현할 수 있는 코드이다.
n = int(input()) - 2
f1 = 1
f2 = 1
for i in range(n):
f2 += f1
f1 = f2 - f1
print(f2)
n을 입력받는데 이미 수열에서 [1, 1]은 지정되어 있기에 2를 빼주고, Fn-2를 변수 f1으로, Fn-1와 Fn을 변수 f2로 지정했다.
피보나치 수가 될 f2에 f1을 더해주고, f1을 f2 - f1으로 지정해주는 코드이다. 이렇게 말하니까 이해하기가 좀 어려운데, 예시를 들어 설명해 보자면,
[1(f1), 1(f2)], [1, 1(f2(2)-f1), 2(f1+f2=f2)], [1, 1, 2(f2(3)-f1), 3(f1+f2=f2)]... 이렇게 되는 것이다.
f1이던 1과 f2던 1이, f2는 f1+f2가 되서 2가 되고, f1은 아까 만든 f2=2에서 f1=1을 빼서 1이 된다. 그 뒤에는 f2가 f1+f2니까 3이 되고, f1은 f2=3에서 f1=1을 빼니까 2가 된다. 이런 식으로 쭉 가다 보면 n번째 피보나치 수를 구할 수 있는 것이다.
백준에 제출해 보았다.
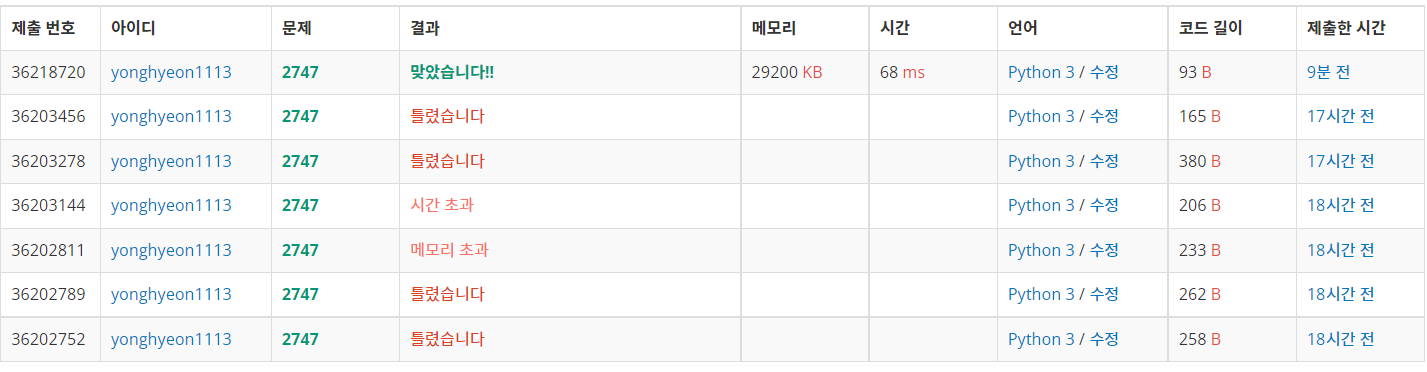
길고 긴 실패 끝에... 드디어 맞았다. 기쁘다.
'PS > Python' 카테고리의 다른 글
| [Python] 백준 21734번(SMUPC의 등장) 문제 풀이 (0) | 2021.12.12 |
|---|---|
| [Python] 백준 2609번(최대공약수와 최소공배수) 문제 풀이 (0) | 2021.12.12 |
| [Python] 백준 23348번(스트릿 코딩 파이터) 문제 풀이 (2) | 2021.12.11 |
| [Python] 백준 10872번(팩토리얼) 문제 풀이 (0) | 2021.12.04 |
| [Python] 백준 10818번(최소, 최대) 문제 풀이 (0) | 2021.12.03 |