지나가던 개발자
[Algorithm] 카라추바 알고리즘 | 빠른 곱셈 | Python 본문
PS를 할 때 빠른 곱셈과 빠른 거듭제곱은 정말로 중요하다. PS를 할 때 뿐만 아니라 그냥 코딩을 할 때에도 중요하다.
카라추바 알고리즘은 빠르게 곱셈을 할 때에 사용되는 알고리즘으로, 보통의 곱셈 알고리즘의 시간 복잡도가 O(n^2)인 데에 반해 카라추바 알고리즘의 시간 복잡도는 O(n^1.585)밖에 나오지 않는다. 혁신인 것이다! O(n^2)와 O(n^1.585)가 차이가 별로 안 난다고 생각할 지도 모르지만, n이 1부터 50까지 커질 때 O(n^2)와 O(n^1.585)의 차이를 보면 다음과 같다.
for n in range(1, 51):
print("When N is", n, "- O(n^1.585):", n**1.585, "O(n^2): ", n**2)
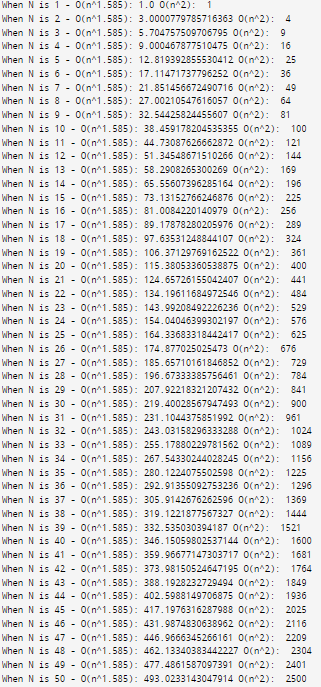
n=2일 때는 약 3과 4 정도로밖에 차이가 나지 않지만, n=50만 되어도 약 493과 2500 정도의 차이가 난다. 이게 n=100이 되면 약 1479와 10000, n=10000이 되면 약 2187762와 100000000 정도까지 벌어진다. 이게 바로 카라추바 알고리즘이 필요한 이유이다.
카라추바 알고리즘에서는 곱셈을 덧셈 몇 번으로 단순화시키는데, 그 과정은 다음과 같다.
x와 y를 B자리수의 n자리수라고 하면, m<n인 정수 m에 대해 x와 y를 이렇게 나타낼 수 있다.
$$ x = x_{1}B^{m} + x_{0} $$
$$ y = y_{1}B^{m} + y_{0} $$
$$ (단, x_{0} < B^{m}, y_{0} < B^{m}) $$
$$ z_{2} = x_{1}y_{1} $$
$$ z_{1} = x_{1}y_{0} + x_{0}y_{1} $$
$$ z_{0} = x_{0}y_{0} $$
이러면 중3때 배웠던 곱셈 공식이 떠오르지 않는가! (a+b)(c+d) = ac+ad+bc+bd이다! 그렇다면 z₁을 이렇게도 나타낼 수 있겠다.
$$ z_{1} = (x_{1}y_{1} + x_{1}y_{0} + x_{0}y_{1} + x_{0}y_{0}) - x_{1}y_{1} - x_{0}y_{0} $$
$$ z_{1} = (x_{1} + x_{0})(y_{1} + y_{0}) - z_{2} - z_{0} $$
이다! 그러면 xy를 곱셈 3번만으로 구할 수 있게 된다.
$$ xy = (x_{1}B^{2m} + x_{0})(y_{1}B^{m} + y_{0}) = z_{2}B^{2m} + z_{1}B^{m} + z_{0} $$
위 식은 원래 곱셈 4번을 통해 구하지만, 아까 z₁을 몇 번의 덧셈으로 나타내었기에 곱셈 3번만으로 구할 수 있게 된다!
아무래도 문자로 해석하기는 어려우니 숫자 1234와 5678을 카라추바 알고리즘을 이용하여 구해보자.
$$ x = 1234, y = 5678, B = 10, m = 2 $$
$$ x = 12*10^{2} + 34 $$
$$ y = 56*10^{2} + 78 $$
$$ z_{2} = 12*56 = 672 $$
$$ z_{0} = 34*78 = 2652 $$
$$ z_{1} = (12+34)(56+78) - 672 - 2652 = 2840 $$
$$ xy = 672*10^{4} + 2840*10^{2} + 2652 = 7006652 $$
그럼 이제 파이썬을 이용하여 이 알고리즘을 코드로 나타내어 보면 다음과 같다. 만약 카라추바 알고리즘이 아직 이해가 가지 않는다면 이해를 못 한 채로 있지 말고, 이 글을 N회독 하면 싫으면 문과에 가던지 언젠가 이해가 될 것이다.
이해가 안 되는 부분은 댓글 남겨 주시면 답변해드립니다~
def karatsuba(x, y):
if len(str(x)) == 1 or len(str(y)) == 1:
return x * y
m = min(len(str(x)), len(str(y))) // 2
a, b, c, d = int(str(x)[:-m]), int(str(x)[-m:]), int(str(y)[:-m]), int(str(y)[-m:])
z2 = karatsuba(a, c)
z0 = karatsuba(b, d)
z1 = karatsuba(a+b, c+d) - z2 - z0
return z2*10**(2*m) + z1*10**m + z0
이 글을 쓰는 데 도움이 되었던 자료들:
카라추바 알고리즘 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 카라추바 알고리즘은 소련의 수학자 아나톨리 알렉세예비치 카라추바가 1960년에 발견하고 1962년에 공개한, 큰 수에 대한 효과적인 곱셈 알고리즘이다. [1][2][3]
ko.wikipedia.org
https://choiseokwon.tistory.com/235
Python Karatsuba(카라추바) 곱셈 알고리즘
Karatsuba 알고리즘 1. 소개 카라추바 알고리즘이란, 큰 수에 대해 효과적인 곱셉 알고리즘이다. (23살에 1주일 만에 발견한 알고리즘) (보통 두 수 곱 시간 복잡도는 $O(n^2)$ 이지만 카라추바 알고리
choiseokwon.tistory.com
[알고리즘] 카라추바의 빠른 곱셈(Karatsuba)
123 × 456 = ? 평소에 일상적으로 계산하던 방법을 분석적으로 풀어써보면 이렇다. 우리는 평소 한 자리에 0부터 9까지의 숫자만 사용하는 십진법을 사용하기 때문에, 각 자리별로 십의 자리 수는
hhlab.tistory.com
https://nearkim.coffee/posts/karatsuba-python-implementation
Karatsuba 알고리즘 구현하기
빠른 곱셈연산을 위한 Karatsuba 알고리즘을 Python으로 구현하기
nearkim.coffee
'Algorithm' 카테고리의 다른 글
| [Algorithm] 비트마스킹 | Python (0) | 2022.12.02 |
|---|---|
| [Algorithm] 분할 정복을 이용한 거듭제곱 | 빠른 거듭제곱 | Python (0) | 2022.10.22 |
| [Algorithm] 오일러 피 함수(Euler's phi function) | 서로소인 자연수의 개수 구하기 | Python (1) | 2022.10.22 |
| [Algorithm] 빅오(Big-O) 표기법으로 시간 복잡도 나타내기 (0) | 2022.08.29 |
| [Algorithm] 1부터 n까지의 합이 {n(n+1)}/2인 이유 (0) | 2022.01.17 |


