지나가던 개발자
[Algorithm] 오일러 피 함수(Euler's phi function) | 서로소인 자연수의 개수 구하기 | Python 본문
[Algorithm] 오일러 피 함수(Euler's phi function) | 서로소인 자연수의 개수 구하기 | Python
KwonYongHyeon 2022. 10. 22. 15:42오일러 피 함수(Euler's phi function, ϕ)은 임의의 양의 정수 n과 서로소인 자연수의 개수를 구하는 함수이다.
1. n이 소수일 때
n이 소수일 때 ϕ(n)은 항상 (n-1)의 값을 가진다. 왜냐하면 소수는 모든 자연수와 서로소이기 때문이다.
$$ n = ab (a, b \in N, a<b) \neq 1 $$
$$ a = 1 \land b > 1 $$
$$ \phi (n) = n-1 $$
2. n이 소수의 거듭제곱일 때
n이 소수 p의 거듭제곱일 때에, ϕ(n)은 다음과 같이 계산된다.
$$ n = p^{k} $$
$$ p = ab(a, b \in N, a<b) \neq 1 $$
$$ a = 1 \land b > 1 $$
$$ \phi (n) = p^{k-1} (p-1) $$
3. m과 n이 서로소일 때
m과 n이 서로소일 때, mn과의 서로소의 개수는 m과의 서로소의 개수와 n과의 서로소의 개수의 곱과 같다,
$$ m \perp n $$
$$ \phi (mn) = \phi (m) \phi (n) $$
오일러 피 함수를 사용하여 임의의 수 n과 서로소인 자연수들의 개수를 살펴보자.
$$ \phi (3) = 2 $$
$$ \phi (27) = 3^{3} = 3^{2} \cdot 2 = 18 $$
$$ \phi (990) = 2 \cdot 3^{2} \cdot 5 \cdot 11 = \phi (2) \phi (3^{2}) \phi (5) \phi (11) = 1 \cdot 6 \cdot 4 \cdot 10 = 240 $$
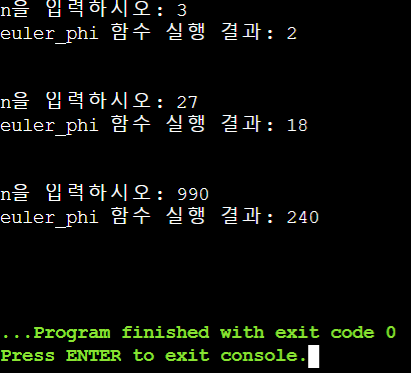
이를 파이썬으로 구현해 보자.
def factorization(x):
d = 2
factorization = []
while d <= x:
if x % d == 0:
factorization.append(d)
x = x / d
else:
d = d + 1
return factorization
def euler_phi(n):
primes = factorization(n)
k = 1
for p in set(primes):
k *= p**(primes.count(p)-1) * (p-1)
return k
조건 1번과 조건 2번에서의 식은 어떤 수의 0승은 항상 1이기에 같은 식이라고 볼 수 있다. 따라서 17번 줄로 일반화된다.
이 글을 쓰는 데 도움이 되었던 자료들:
https://rkdxowhd98.tistory.com/135
Algorithm in A..Z - Euler's phi (오일러 피 함수)
개념 오일러의 피 함수는 N이 주어 졌을 때 1 ~ N의 숫자중 N과 서로소인 숫자의 개수를 찾는 함수이다. 작동원리 1. p가 소수인 경우 소수인 경우 약수가 1과 자기 자신밖에 없으므로 자기 자신을
rkdxowhd98.tistory.com
https://zoosso.tistory.com/243
오일러 피(파이) 함수(Euler's phi function)
오일러 피(파이) 함수 ϕ(n) 1~n까지의 수 중에서 n과 서로소인 수의 갯수 ※ 서로소 관계: 두 수 a, b의 공약수가 1뿐인 두 정수를 의미한다. ϕ(1) = 1 (1은 1과 서로소) ϕ(8) = { 1, 3, 5, 7 } =..
zoosso.tistory.com
https://ko.wikipedia.org/wiki/%EC%86%8C%EC%88%98_(%EC%88%98%EB%A1%A0)
소수 (수론) - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 각각의 자리에 놓인 숫자와 소수점을 통해 나타낸 실수(小數)에 대해서는 소수 (기수법) 문서를 참고하십시오. 좌측은 소수, 우측은 합성수. ...소수란 1보다 큰
ko.wikipedia.org
'Algorithm' 카테고리의 다른 글
| [Algorithm] 비트마스킹 | Python (0) | 2022.12.02 |
|---|---|
| [Algorithm] 분할 정복을 이용한 거듭제곱 | 빠른 거듭제곱 | Python (0) | 2022.10.22 |
| [Algorithm] 카라추바 알고리즘 | 빠른 곱셈 | Python (1) | 2022.09.09 |
| [Algorithm] 빅오(Big-O) 표기법으로 시간 복잡도 나타내기 (0) | 2022.08.29 |
| [Algorithm] 1부터 n까지의 합이 {n(n+1)}/2인 이유 (0) | 2022.01.17 |

