지나가던 개발자
[Mathematics] 삼차방정식의 근과 계수와의 관계 본문
이차방정식에는 근과 계수와의 관계가 있다. 바로 이차방정식 ax²+bx+c 의 두 근 α, β에서 α+β = -b/a, αβ = c/a 라는 것이었다.
삼차방정식에도 그러한 근과 계수와의 관계가 있다. 삼차방정식 ax³+bx²+cx+d의 세 근 α, β, γ에서 α+β+γ = -b/a, αβ+βγ+αγ = c/a, αβγ = -d/a라는 것이다.
한번 증명해 보겠다.
삼차방정식 ax³+bx²+cx+d의 세 근이 α, β, γ라는 말은, ax³+bx²+cx+d = a(x-α)(x-β)(x-γ) 라는 뜻이다. 따라서 좌변과 우변을 비교해주면 삼차방정식의 근과 계수와의 관계를 유도할 수 있는 것이다.
우변을 풀면 a{x³-(α+β+γ)x²+(αβ+βγ+αγ)x - αβγ} = ax³-a(α+β+γ)x²+a(αβ+βγ+αγ)x-aαβγ 이다.
ax³-a(α+β+γ)x²+a(αβ+βγ+αγ)x-aαβγ = ax³+bx²+cx+d 이므로 x²의 계수부터 비교해 보자면,
-a(α+β+γ) = b 이므로 α+β+γ = -b/a 이다.
a(αβ+βγ+αγ) = c 이므로 (αβ+βγ+αγ) = c/a 이다.
-aαβγ = d 이므로 αβγ = -d/a 이다.
Feat.

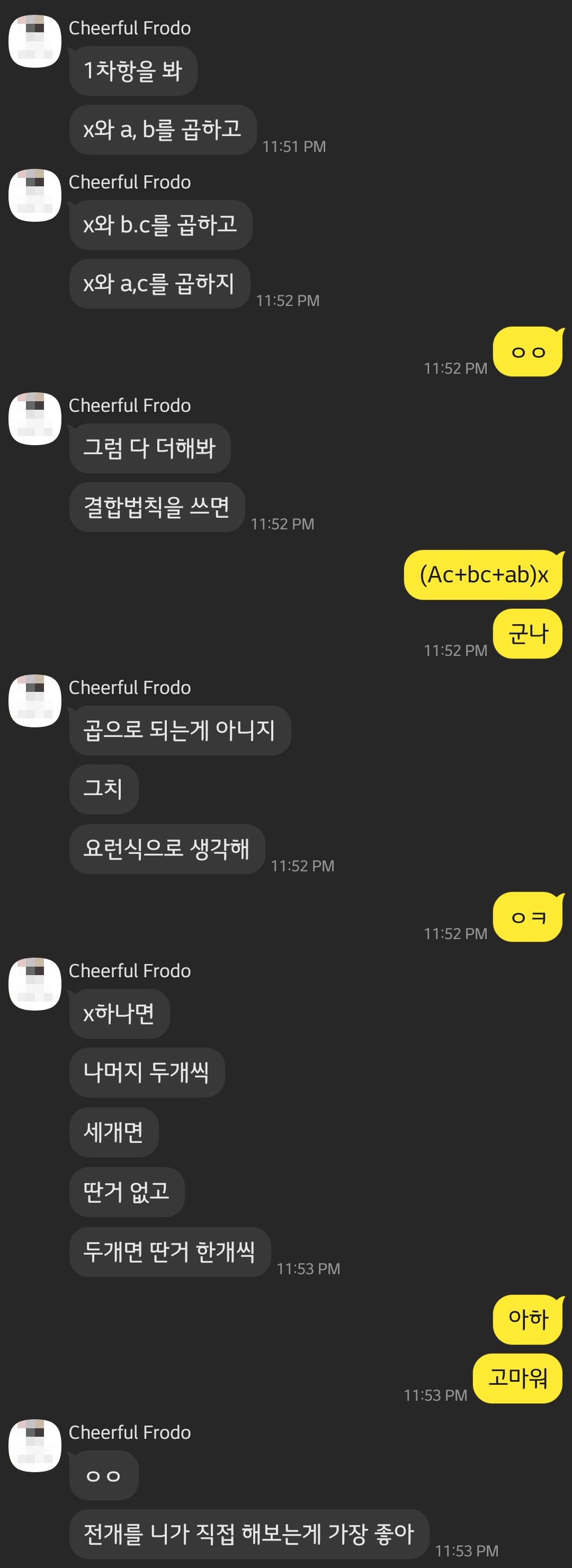
맨 처음에 글을 썼을때(αβ+βγ+αγ) = c/a를 (αβ)(β)(αγ) = c/a라고 썼었다.. 친구가 보고 알려줘서 알았다. 고마워!
친구 유튜브 - https://youtube.com/channel/UCcMxwEvSuAzQdzkp4XPiDiQ
자작가871
😈Prince of Darkness 소설 쓰는 채널 자작가 871입니다. 제 친구 '코더 용현'과 저 많은 사랑 부탁드립니다. 그리고 이 채널에선 소설 재미없으면 보지말기 나한테 칭찬만 하기 그냥 재미 없어도 보기
www.youtube.com
친구 유튜브에 구독 좋아요 부탁드려요!
'Mathematics' 카테고리의 다른 글
| [Mathematics] 유클리드 호제법의 증명 (0) | 2022.09.04 |
|---|---|
| [Mathematics] 실수 a, b에 대하여 a²+b²≥ab인 이유 증명 (0) | 2022.02.08 |
| [Mathematics] 삼차방정식 x³=1의 허근 ω의 성질 (0) | 2022.02.04 |
| [Mathematics] 이차방정식의 짝수 공식의 유도 (0) | 2022.01.24 |
| [Mathematics] 음수의 제곱근의 성질 l a<0, b<0이면 √a√b = -√ab, a>0, b<0이면 √a / √b = -√a/b인 (0) | 2022.01.24 |
