지나가던 개발자
[Mathematics] 삼각형의 닮음을 이용한 피타고라스 정리의 증명 본문
혼자서 끄적끄적 하다가 찾은 피타고라스 정리의 증명이다. 뭐 물론 내가 증명하기 전에도 여러 사람들이 같은 증명법으로 증명했겠지만, 그래도 내가 찾은 방법이니 블로그에 올려본다.
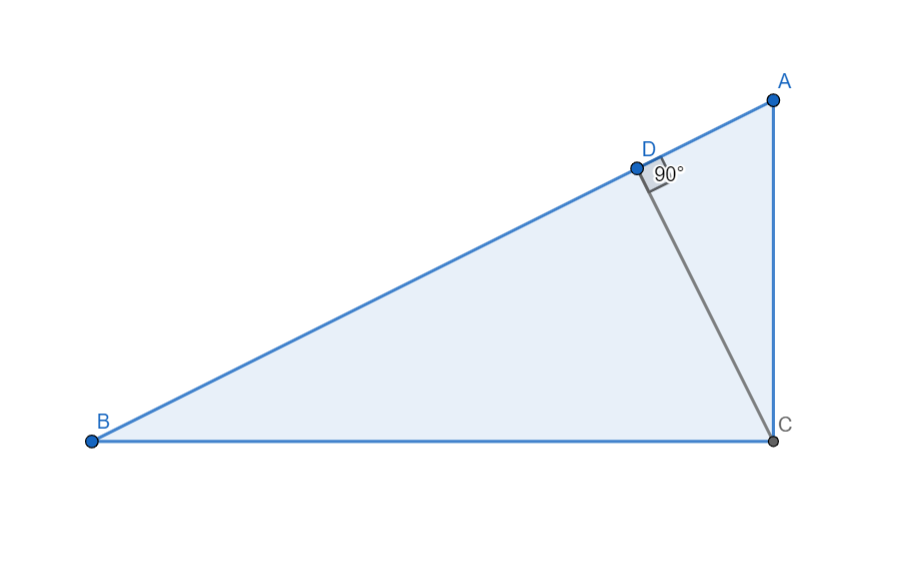
각 C가 직각인 직각삼각형 ABC에서 다음과 같이 나타내어 보자.
$$ \overline{bc} = a $$
$$ \overline{ac} = b $$
$$ \overline{ab} = c $$
$$ \overline{bd} = m $$
$$ \overline{ab} = n $$
그런데, 다음과 같이 삼각형 DBC와 삼각형 DCA, 삼각형 CBA가 닮음임을 보일 수 있다.
$$ \angle{A} + \angle{B} = 90° $$
$$ \angle{BCD} = \angle{A}, \angle{ACD} = \angle{B} $$
$$ \bigtriangleup{DBC} ∽ \bigtriangleup{DCA} ∽ \bigtriangleup{CBA} (AA닮음) $$
따라서 다음과 같은 비례식이 성립한다.
$$ b : m = c : b $$
$$ a : c = n : a $$
따라서, m과 n은 이렇게 나타낼 수 있다.
$$ m = \frac{b^{2}}{c} $$
$$ n = \frac{a^{2}}{c} $$
m+n=c 이므로 다음과 같은 방정식을 풀이, 피타고라스 정리가 성립한다.
$$ n + m = \frac{a^{2}+b^{2}}{c} = c $$$$ a^{2} + b^{2} = c^{2} $$
'Mathematics' 카테고리의 다른 글
| [Mathematics] 파푸스의 중선정리의 증명 (0) | 2023.03.13 |
|---|---|
| [Mathematics] 삼각형의 한 변과 양 끝각을 알 때의 넓이 구하기 (0) | 2022.10.21 |
| [Mathematics] 유클리드 호제법의 증명 (0) | 2022.09.04 |
| [Mathematics] 실수 a, b에 대하여 a²+b²≥ab인 이유 증명 (0) | 2022.02.08 |
| [Mathematics] 삼차방정식 x³=1의 허근 ω의 성질 (0) | 2022.02.04 |


